Урок 24 Бесплатно Порядок выполнения действий
Изучая числовые и буквенные выражения, способы упрощения выражений, свойства арифметических операций, мы рассматривали в основном простые выражения, значение которых найти было несложно.
Сегодня на уроке мы будем рассматривать выражения, в которых содержатся сразу несколько арифметических операций и несколько пар скобок.
Выясним, в какой последовательности необходимо выполнять математические операции при нахождении значения выражения.

Узнаем, какие действия называют действиями первой и второй ступени, зачем нужны скобки.
Разберем множество различных примеров, которые позволят нам лучше усвоить данную тему.
Порядок выполнения действий
Любой человек каждый день решает множество различных задач: простых и сложных.
Многие из них решаются по определенным правилам- алгоритмам.
У меня есть дополнительная информация к этой части урока!
Алгоритм- это определенная последовательность действий.

Алгоритм задает не только совокупность действий, но и порядок их выполнения.
Например, алгоритмом можно считать инструкцию по эксплуатации какого-либо прибора, рецепт приготовления блюда в кулинарной книге, порядок действий при включении компьютера, порядок выполнения практической работы, расписание уроков, режим дня, правила дорожного движения и многое другое.
Приведем пример простейшей последовательности действий (алгоритма) из повседневной жизни.
Порядок действий (алгоритм) открывания замка ключом.

Чтобы получить верный результат, необходимо соблюдать определенный порядок действий.
Если мы изменим порядок действий в рассмотренном алгоритме открывания замка ключом, то открыть его не получится.

На самом деле, не получится сначала вставить ключ в замочную скважину, а затем найти этот ключ, а если не вставить ключ в замочную скважину, то, конечно же, не удастся повернуть ключ и вытащить его.
С алгоритмами мы уже не раз встречались на наших уроках, решая задачи и уравнения, рассматривая различные правила и свойства, совершая вычисления в столбик и др.
Выясним зависит ли значение выражения от порядка выполнения арифметических операций, обязательно ли выполнять действия в определенном порядке.
Рассмотрим следующий пример:
Катя и Федя решали пример, в котором необходимо было найти сумму числа 24 и произведения чисел 8 и 2.
Катя записала пример: 24 + 8 ∙ 2 и принялась выполнять арифметические действия по порядку.
Первым делом она нашла сумму чисел 24 и 8.
Сложив 24 и 8, у нее получилось число 32.
24 + 8 = 32.
Затем полученный результат (число 32) она умножила на 2.
В итоге у нее получилось:
32 ∙ 2 = 64.
Ответ: 64.
Федя записал пример: 24 + 8 ∙ 2 и стал решать его иным способом.
Сначала он нашел произведение чисел 8 и 2.
Умножив 8 на 2, у него получилось число 16.
8 ∙ 2 = 16.
Затем к 24 прибавил полученное произведение.
В итоге получил следующее равенство:
16 + 24 = 40.
Ответ: 40.
Исходные выражения, которые записали Катя и Федя, были одинаковые (содержали определенную последовательность чисел и знаков).
Дети меняли только порядок следования математических операций.
В итоге получили различные значения одного и того же выражения.
Получается, что порядок выполнения арифметических действий влияет на результат вычислений.
Чуть позже мы выясним, кто же решил пример правильно: Катя или Федя.
Пройти тест и получить оценку можно после входа или регистрации
Фокус на 7
Вам понадобятся несколько игральных кубиков (костей). Скажите ребёнку, что, сколько бы костей он ни выбросил, вы сразу же скажете сумму точек на их верхних и нижних гранях — даже несмотря на то, что низ кубиков не видно.
Секрет прост: кубики устроены таким образом, что сумма точек на верхней и нижней поверхностях всегда равна 7. Таким образом, чтобы узнать правильный ответ, достаточно умножить количество брошенных кубиков на 7.
Предложите ребёнку показать фокус брату или сестре, бабушке с дедушкой, друзьям. Пусть школьник меняет число кубиков. Это поможет ему закрепить в памяти умножение на 7.
Совет в запоминании №1
Большую роль в усвоении таблицы умножения играет понимание смысла умножения. Объясните ребёнку смысл действия умножения и научите этим пользоваться при вычислениях.
Умножение – это сумма одинаковых слагаемых.
8 x 3 – это значит, что число 8 мы должны взять 3 раза: 8 х 3 = 8 + 8 + 8
Понимая смысл множителя, ребёнок сможет найти результат даже в ситуации, когда он забыл какой-то случай из таблицы.
Например, забыв результат умножения числа 4 на 8, можно заменить умножение сложением и найти произведение: 4 х 8 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32.
Важно знать переместительное свойство умножения (от перестановки множителей произведение не меняется), тогда результат можно найти ещё быстрее: 4 х 8 = 8 х 4 = 8 + 8 + 8 + 8 = 32
Умножать можно с помощью рук Умножение на 9
Для этого положите руки ладонями вверх, пальцы разогните. Мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните тот палец, на какое число нужно умножить 9. Например, нужно 9х3. Загибаете 3 палец. Все пальцы слева (их 2 — это десятки), пальцы справа (их 7) — единицы. Соединяем десятки и единицы, получаем — 27.
Вычисление произведения любых однозначных чисел больше, чем 5
Способ 1
Пронумеруйте мысленно пальцы на обеих руках. Мизинец — 6, безымянный — 7, средний — 8, указательный — 9, большой — 10 (на то он и БОЛЬШОЙ, чтобы выражать самое БОЛЬШОЕ число).
Допустим, вы хотите узнать, сколько будет 8 х 7. Соедините вместе средний палец левой руки (8) с безымянным правой (7), как показано на рисунке. А теперь считайте. Два соединённых пальца плюс те, что под ними, указывают на количество десятков в произведении. В данном случае — 5. Число пальцев, оказавшихся над одним из сомкнутых пальцев, умножьте другим сомкнутым пальцем. В нашем случае 2 х 3 = 6. Это — число единиц в искомом произведении. Десятки складываем с единицами, и ответ готов — 56.
Способ 2
Например, нужно выяснить сколько будет при счете 7х7. Загнём на левой руке столько пальцев, на сколько первый множитель больше 5, а на правой руке столько пальцев, на сколько второй множитель больше 5.
В данном случае будет загнуто по 2 пальца. Если сложить количество загнутых пальцев и перемножить количество не загнутых, то получится соответственно число десятков и единиц искомого произведения, т.е. 49. Если этим способом вычислять произведение 6х7, то получится 3 десятка и 12 единиц, т.е. 30+12=42
Проверьте и убедитесь, что эти способы действительно работают.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения: 5 + 2 − 2 − 1 Решение
Показать решение Задание 2. Найдите значение выражения: 14 + (6 + 2 × 3) − 6 Решение
Показать решение Задание 3. Найдите значение выражения: 486 : 9 − 288 : 9 Решение
Показать решение Задание 4. Найдите значение выражения: 756 : 3 : 4 × 28 Решение
Показать решение Задание 5. Найдите значение выражения: 807 : 3 − (500 − 58 × 4) Решение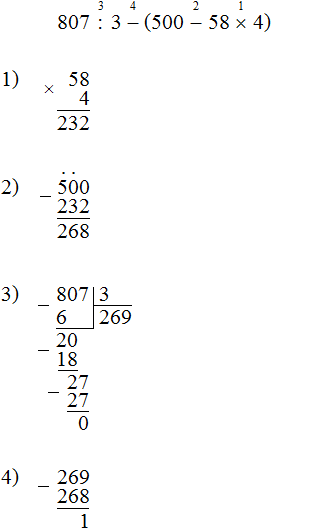
Дополнительные примеры
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Полностью пример записываем так:
10 + 15 – 6 – 8 = 25 – 6 – 8 = 19 – 8 = 11
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
Полностью пример записываем так:
10 – 15 : 3 + 6 • 8 = 10 – 5 + 6 • 8 = 10 – 5 + 48 = 5 + 48 = 53
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например, 
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.

Полностью пример записываем так:
(25 – 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53
Например, 
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.
Счет на пальцах
Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы — это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.
Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:
- Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
- Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.
- Оставшееся количество пальцев слева будет соответствовать десяткам, справа — единицам. В нашем примере — 4 пальца слева и 5 справа. Ответ: 45.
Да, действительно, решение быстрое и наглядное! Но это — из области фокусов. Правило действует только при умножении на 9. А не проще ли, для умножения 5 на 9 выучить таблицу умножения? Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.
Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.
Методы обучения вычислениям в математике 3 класса
В 3 классе ученики начинают изучение основ вычислительной математики: сложения, вычитания, умножения, деления. Но как же методы обучения помогают им развиваться в этой области знаний?
Первый метод — это игры и задания на скорость, которые позволяют ученикам ускорить реакцию и привить им любовь к математике. Например, в игре «Быстрый калькулятор» ученики должны на скорость решать примеры и делать это правильно.
Второй метод — это использование разных предметов в качестве наглядных материалов для изучения математики. Например, ребенок может разбирать яблоки или печенье на части, чтобы понять, как работает деление.
Третий метод — это укрепление навыков вычисления через повторение. Учитель может давать детям повторять примеры несколько раз, пока они не научатся их решать на автомате.
Четвертый метод — это использование интерактивных игр и программ в обучении, которые помогают ученикам лучше понимать математические концепции. Это такие игры, как «Mathway» или «Золотая рыбка», которые дают возможность ученикам применить полученные знания в практических ситуациях.
В итоге, эти методы обучения вычислениям помогают ученикам лучше понимать и запоминать математические концепции, а также развивать навыки решения проблем.
Главные правила по теме
Говоря о главных и неглавных математических действиях, нужно сказать, что четыре основных действия можно свести к двум: сложение и умножение. Если вычитание и деление представляется для школьников сложным, правила сложения и умножения они запоминают быстрее. Действительно, выражение 5 – 2 можно записать иначе:
2 + х = 5.
Аналогично:
8 : 2 = у × 2 = 8.
В случаях с умножением действуют правила, схожие со свойствами сложения: от перестановки множителей произведение не изменится:
5 × 4 = 4 × 5.
При решении сложных задач первое действие — то, которое выделено скобками, затем — деление или умножение, потом все остальные действия по порядку.
Когда нужно решить примеры без скобок, вначале выполняется умножение или деление, далее — вычитание либо сложение.
Да какая разница?
Действительно, настолько ли это важно – какое действие в примере выполнить первым, какое вторым?
Рассмотрим примеры:
10 – 5 + 2 = ?
Если мы будем выполнять действия по порядку, получим:
- 10 – 5 = 5;
- 5 + 2 = 7.
Попробуем иначе:
- 5 + 2 = 7;
- 10 – 7 = 3.
Получили два разных ответа. Но так быть не должно, следовательно, порядок выполнения действий имеет значение. Тем более, если в выражении имеются скобки:
25 – (18+2) = ?
Пробуем решить двумя способами:
- 25 – 18 + 2 = 9;
- 25 – 20 = 5.
Ответы разные, а для того чтобы определить порядок действий, в выражении стоят скобки – они показывают, какое действие нужно выполнить первым. Значит, правильным будет такое решение:
- 18 + 2 = 20;
- 25 – 20 = 5.
Другого решения у ответа у примера быть не должно.
Итак:
Правило первое: Математические действия в выражении выполняются по порядку, начиная с левого, направо.
Правило второе: Если в выражении есть скобки, действие в скобках выполняется в первую очередь, а затем следуют действия по порядку, слева направо.
Деление двузначного числа на однозначное
Ребята, вы меня узнали? Люблю наряжаться на маскарад. Вот прицепил такие усы, думал, что буду похож на фокусника. Чудеса начинаются.
Такие задания называют примерами с «усиками». Да, да, но усики носят не люди, кто делит, а сами примеры. Рисовать их нужно простым карандашом, а когда научитесь быстро считать, то просто представляйте в голове.
Устное деление двузначного на однозначное
Задание 1.
Пусть надо решить, сколько будет
К «усикам» запишем такие два слагаемых, которые делятся на 8, а в сумме дают 96.
Самое главное — это не ошибиться в подборе первого «усика». Надо запомнить, что он всегда больше, чем второй. Ищем его, умножая 8 на 10. Если не подойдет, то будем умножать на 20, на 30. Главное, чтобы было круглое число.
Все понятно? Будем тренироваться.
Задание 2.
Задание 3.
Попробуем разделить 90 на два. «Первый усик» явно не 20, тогда второй будет 70. Знаем, что «второй усик» не может быть больше первого.
Вижу, что не 60, потому что 30 разделить на два — это не табличный случай.
Следовательно, 2 ∙ 40 = 80. Значит «первый усик» предположительно 80. «Второй усик» тогда найдем вычитанием: 90 – 80 = 10. Десять разделить на два, это таблица.
Как думаете, вы справитесь с делением? Когда встречаете случаи, где двузначное число делится на однозначное, и примеры не относятся к таблице умножения, то решайте подбором «усиков». Разбивайте делимое на подходящие слагаемые. Их можно записать суммой в скобочках, а при делении использовать правило деления суммы на число.
Решите задачу.
Таня выполнила 96 примеров, а Коля в 4 раза меньше. Сколько примеров решил Коля?
Чтобы ответить на вопрос задачи, надо выполнить действие деления.
96 : 4 =
«Усиками» будут 80 и 16, получается сумма 80 + 16. Значит, каждое из этих слагаемых разделите на 4, а частные сложите.
Ответ: 24
Деление столбиком двузначное на однозначное
Письменное деление уголком просто невозможно усвоить без блестящего знания таблицы умножения. Это просто трата времени и нервов. В древности в римских школах ее заучивали хором на распев. Знаете ответы на «отлично», тогда переходите на примеры деления в столбик.
Задание 1.
Пусть надо 84 разделить на три. Посмотрите на запись. Такой значок означает деление уголком. Уголок имеет наверху делитель, на который делим. Под чертой — результат, который ищем. Он называется частным.
Нам надо узнать, чему равно частное. Но прежде определим, сколько цифр будет в результате. Это очень важный шаг, поэтому упускать его нельзя. Как мы будем это делать? Посмотрите на первую цифру. Это восьмерка. Восемь больше трех. Значит, она может дать нам полноценную цифру в частном. Ставим точку. После восьмерки еще одна цифра, это значит, что частное — двузначное число. Под чертой в уголке карандашом поставьте вторую точку.
Первое неполное делимое — восьмерка. Начинаем ее делить на три, ищем табличный случай. Легче всего уменьшать 8 на единицу.
8 – 1 = 7. В таблице нет деления семи на три.
Уменьшаем еще на 1.
7 – 1 = 6. Шесть делится на три, получается — по два. Записываем 2 в частное под чертой.
Теперь мы должны понять, сколько не разделили. Ведь разделили всего шесть.
А надо было разделить восемь.
Два осталось неразделенным. Это остаток. Он должен быть меньше делителя.
Давайте проверим: два меньше трех.
Да, действительно. Мы сделали все правильно. Этот шаг очень важен. Не забывайте сравнивать остаток с делителем.
После этого сносим следующую цифру с тем, чтобы получить новое неполное делимое
Обратите внимание: нужно писать каждую цифру в своей клетке. Получается неполное делимое 24
Ответ: 28.
Задание 2.
Решите пример столбиком 96 : 4 =
Проверьте:
Ура! Наш математический маршрут пройден. Знания-сокровища из цветных лент превратились в волшебную радугу. Что же у нас вышло, что мы унесем в нашем сундуке. Закончите предложения:
Деление целых чисел
Пример 1. Найти значение выражения 12 : (−2)
Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.
12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6
Обычно записывают покороче:
12 : (−2) = −6
Пример 2. Найти значение выражения −24 : 6
Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.
−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4
Запишем решение покороче:
−24 : 6 = −4
Пример 3. Найти значение выражения −45 : (−5)
Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
−45 : (−5) = |−45| : |−5| = 45 : 5 = 9
Запишем решение покороче:
−45 : (−5) = 9
Пример 4. Найти значение выражения −36 : (−4) : (−3)
Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.
Разделим −36 на (−4), и полученное число разделим на −3
Первое действие:
−36 : (−4) = |−36| : |−4| = 36 : 4 = 9
Второе действие:
9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3
Запишем решение покороче:
−36 : (−4) : (−3) = 9 : (−3) = −3
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Математические действия с нулем
Круглый нуль такой хорошенький, Но не значит ничегошеньки.
В примерах нуль как число не встречается, но он может быть результатом какого-либо промежуточного действия, например:
5 × (8 : 2 – 4) = ?
- 8 : 2 = 4;
- 4 – 4 = 0;
- 5 × 0 = ?
При умножении на 0 правило гласит, что в результате всегда получится 0. Почему? Объяснить можно просто: что такое умножение? Это одно и то же число, сложенное с себе подобным несколько раз. Иначе:
0 × 5 = 0 + 0 + 0 + 0 + 0 = 0;
Деление на 0 бессмысленно, а деление нуля на любое число даст в результате всегда 0:
0 : 5 = 0.
Да и как может быть иначе, когда делить-то нечего? Если у вас нет яблок, поделиться с друзьями вам нечем.
Напомним другие арифметические действия с нулем:
а + 0 = а;
0 + а = а (от перестановки слагаемых сумма не меняется);
а – 0 = а;
0 – а = — а (число, противоположное вычитаемому).
Порядок выполнения действий
Простак гуляет, улыбается, считает, веселит друзей. У него свой способ выполнения действий. Он много знает, но не разговаривает, а показывает жестами.
У каждого из нас собственная программа выполнения действий. Иногда расписание меняется, но некоторый порядок менять нельзя. Вы просыпаетесь утром, сначала делаете зарядку, после убираете спальное место. А случается так — сразу застилаете постель, а зарядку выполняете только днем. Но выйти зимой на улицу без обуви и пальто вы не можете, поэтому всегда сначала одеваетесь, лишь потом идете гулять. Гномы перед поиском полезных ископаемых обязательно завтракают.
Нужны ли в математике правила порядка выполнения определенных действий? Простак показал жестом, что примеры со сложением и вычитанием надо решать слева направо, а не наоборот. Нарушение порядка дает неверный ответ.
Порядок выполнения действий друг за другом.
Ниже в примере встречаются все основные виды арифметических операций. По правилу умножение и деление решаются раньше, чем сложение и вычитание. Поэтому первым действием разделим пятнадцать на три, затем умножим шесть на четыре.
В математике есть способ, который показывает, что решается раньше других действий. Нарисуйте скобки — выполните первым вычитание.
Как найти правильный ответ в таких примерах:
Сначала решайте выражения, записанные в скобках;
Далее действия второй ступени — умножение и деление по порядку;
А первой ступени — сложение и вычитание решайте последними действиями.
Алгоритм выполнения действий запишите схемой:
Будьте внимательны к выполнению порядка, чтобы не допускать ошибки.
Ребята, наше путешествие подошло к концу. Гномики прощаются с вами и желают учиться на «отлично».
До скорой встречи!
Дробная черта
Дробная черта в выражении может быть заменена на знак деления, в этом случае, всё что было над и под дробной чертой надо взять в скобки. Например:
Знак деления в выражении можно заменить дробной чертой только в том случае, если это не нарушает порядок действий. Например, выражение:
нельзя заменить на
потому что такая замена нарушит порядок действий в данном выражении.
| 20 : 4(2 + 3) ≠ | 20 | ; |
| 4(2 + 3) |
| 20 | = 20 : (4(2 + 3)). |
| 4(2 + 3) |
Дробная черта в выражении заменяет скобки и означает, что надо вычислить отдельно выражение, стоящее в числителе, и отдельно выражение, стоящее в знаменателе, и первый результат разделить на второй.
Как выучить деление и умножение с ребенком
Самый элементарный метод, с помощью которого можно научиться умножать и делить, представлен наглядной демонстрацией разделения предметов на равные части или же увеличения этих долей. В роли предметов, которые используются в качестве обучающего реквизита, должны выступать предметы, вызывающие в уме школьника интерес.
Умножение и деление однозначных чисел
Для деления однозначных чисел на однозначные лучше всего использовать таблицу умножения, но перед этим следует объяснить своему чаду, что деление – это действие, противоположное умножению. Сделать это можно с помощью любого правильного деления натуральных чисел, к примеру, 2 умножить на 4 будет 8. Придерживаясь данного примера, показать карапузу делительный процесс:
- разделить 8 на любой множитель, например, на число 2;
- в ответе получится 4, то есть множитель, который не был использован при делении.
Таким методом также делятся многозначные (двухзначные) числа на однозначные. А для того, чтобы освоить процесс умножения однозначных чисел, вместе с малышом достаточно лишь постепенно учить таблицу умножения.
Алгоритм деления однозначных чисел
Умножение и деление двузначных чисел
В целях разъяснения дошкольнику процесса умножения двухзначных цифр опытные педагоги рекомендуют прибегать к итальянскому методу или методу «решетки». Для начала следует на листе бумаги начертить мини-таблицу два на два: одно число записать по длине, а другое – по ширине таблицы. Каждую клетку нужно разделить по диагонали ровной линией, после чего в образовавшиеся треугольники вписать результат умножения чисел (отдельно десятки, отдельно единицы).
Далее вместе с ребенком сложить «произведения» строго по диагонали, результат подписать. Произведение будет равно значению, которое образуется в процессе чтения цифр снизу вверх и направо.
Некоторые родители предпочитают использовать китайско-японский способ умножения в процессе обучения своих детей. Он может показаться более сложным, чем метод «решетки», но на деле все не так страшно. Следует всего лишь нарисовать цифры линиями, посчитать «узлы», которые образовались при пересечении, и «собрать» из них произведение. В процессе подсчета учитываются следующие моменты:
- количество узлов, которые получились при пересечении линий, обозначающих десятки перемножаемых чисел = количество сотне произведения;
- узлы, получившиеся при пересечении прямых, обозначающих единицы и десятки умножаемых цифр = количество десятков произведения.
Обратите внимание! Что касается количества узлов, образовавшихся путем пересечения линий, которые обозначают единицы умножаемых чисел, то оно равняется количеству единиц произведения. Если ребенок еще не проходил метод деления двухзначных цифр «столбиком», то нужно объяснить ему на более простом языке
Для примера можно взять 66/3. Число 64 раскладываем на цифры, которые устно можно поделить на 3:
Если ребенок еще не проходил метод деления двухзначных цифр «столбиком», то нужно объяснить ему на более простом языке. Для примера можно взять 66/3. Число 64 раскладываем на цифры, которые устно можно поделить на 3:
64 = 30 + 30 + 6.
Малышу сразу все станет понятно: 30 и 6 мы сможем поделить на 3, после чего нужно будет только сложить результаты, т. е. 66 / 3 = 10 (получили в процессе деления 30 на 3) + 10 (30 поделили на 3) + 2 (6 поделили на 3).
66 / 3 = 22. Здесь не был использован метод разделения в столбик, но карапуз сразу поймет ход рассуждений и выполнит простые вычисления без труда.
Основной порядок выполнение действий для простых выражений
Умножаем
Что такое умножение? При умножении второе число показывает, сколько раз нужно прибавить первое число к самому себе. На рисунке в каждом ряду по 13 человек, всего девять рядов. Чтобы вычислить общее количество людей, необходимо девять раз прибавить 13. В результате получается произведение 13 x 9.

Не имеет значения, в каком порядке перемножаются числа. Ответ будет таким же. Вот два способа вычисления продукта
Умножение на 10, 100, 1000 Чтобы умножить целое число на 10, 100, 1000 и т.д., просто добавьте один ноль (0), два ноля (00), три ноля (000) и т.д. Номер находится на правой стороне.

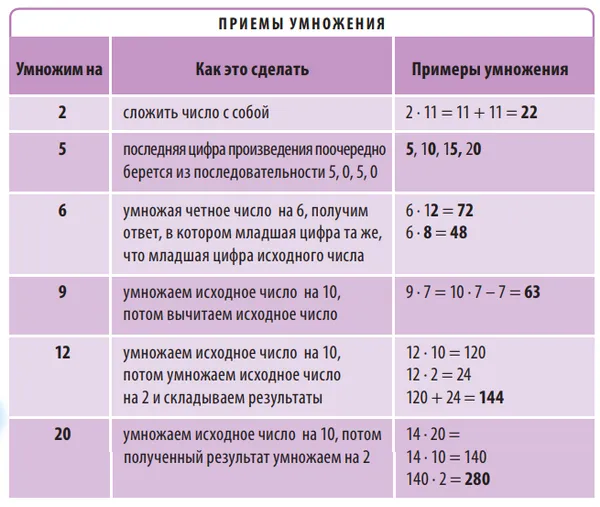
Методы распространения. Некоторые числа легко перемножаются, если знать некоторые специальные приемы. В этой таблице показаны приемы быстрого умножения для 2, 5, 6, 9, 12 и 20.
Публикация «Умножение числа нуль и на нуль, Деление нуля» размещена в разделах
- Математика. Деление чисел. Конспекты уроков
- Математика. Умножение. Конспекты уроков
- Счёт. Цифры и числа, количество
- Темочки
Планируемые результаты: учащиеся научатся выполнять умножение 0 на число, число на 0, делить 0; пользоваться таблицей умножения и деления; решать задачи изученных видов; оценивать правильность выполнения действий.
Оборудование: карточки для игры “Почтальон”; таблица с геометрическими фигурами, раздаточный материал, персональный компьютер, медиа-проектор, учебник «Математика» М. Н. Перова (4 класс).
Тип урока: новая тема.
Вид урока: урок-игра.
Вычисления с дробями, степенями и сложными функциями
Это сложные случаи вычислений, которые не рассматриваются в рамках начальной школы.
Действия с дробями
Умножение простых дробей друг на друга не представляется сложными, достаточно лишь перемножить числитель на числитель, а знаменатель – на знаменатель.
Пример:
- 2 × 3 = 6 — числитель
- 5 × 8 = 40 — знаменатель
\({{2}\over{5}} × {{3}over\{8}} = {{6}over\{40}}\)
После сокращения получаем:\({{6}over\{40}}\) = \({{3}over\{20}}\).
Деление простых дробей не так сложно, как кажется на первый взгляд. Достаточно лишь преобразовать задачу – превратить ее в пример с умножением. Сделать это просто – нужно перевернуть дробь так, чтобы знаменатель стал числителем, а числитель – знаменателем.
Пример:
- 2 × 5 = 10;
- 8 × 3 = 24.
Действия со степенями
Если в задаче встречается число, представленное в виде степени, его значение вычисляется прежде всех остальных (можете представить, что оно заключено в скобки – а действия в скобках выполняются первыми).
Пример:
(5² – 7) : 3 = ?
- 5² = 5 х 5 = 25;
- 25 – 7 = 18;
- 18 : 3 = 6.
(5² – 7) : 3 = 6.
Преобразовав число, представленное в виде степени, в обычное выражение с действием умножения, решить пример оказалось просто: сначала умножение, затем вычитание (потому что в скобках) и деление.
Действия с корнями, логарифмами, функциями
Поскольку такие функции изучаются только в рамках старшей школы, рассматривать их мы не будем, достаточно только сказать, что они, как и в случае со степенями, имеют приоритет при вычислении: сначала находится значение данного выражения, затем порядок вычислений обычный – скобки, умножение с делением, далее по порядку слева направо.
Сложение двоичных чисел
Правила сложения двоичных чисел похожи на привычные нам: сложение происходит поразрядно справа налево, при этом важно помнить о переносе чисел в новый разряд. В десятичной системе у нас всего 10 цифр: от 0 до 9
Когда мы складываем 1 и 9, у нас получается переполнение, так как больше 9 в одном разряде нельзя записать. Поэтому мы переносим единицу в следующий, получаем 10
В десятичной системе у нас всего 10 цифр: от 0 до 9. Когда мы складываем 1 и 9, у нас получается переполнение, так как больше 9 в одном разряде нельзя записать. Поэтому мы переносим единицу в следующий, получаем 10.
Двоичная система работает аналогично: чтобы понять, как складывать числа, нужно помнить об этом переполнении. Всего в двоичной системе две цифры — 0 и 1. Если сложить 1 и 1, мы получим переполнение, а значит, единица пойдёт в следующий разряд, результатом станет 10 (только не «десять», а «один-ноль»).
Если представить правила сложения двоичных чисел в общем виде, получим такую таблицу:
Изображение: Skillbox Media
Но лучше разобраться на примерах.
Пример 1. Давайте сложим 1100 и 101.
Изображение: Skillbox Media
Рассмотрим пример подробнее. Как мы уже упоминали ранее, сложение происходит справа налево. Разряды считаются тоже справа налево:
- Первый: 0 + 1 = 1.
- Второй: 0 + 0 = 0.
- Третий: 1 + 1 = 10 — переполнение, единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 10 — добавляем единицу из прошлого разряда, получаем переполнение, единица переходит в следующий разряд.
- Пятый: 0 + 0 + 1 = 1 — единица пришла из предыдущего разряда.
Пример 2. Сложим 1111 и 111.
Изображение: Skillbox Media
Теперь поразрядно:
- Первый: 1 + 1 = 0 — единица переходит в следующий разряд.
- Второй: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Третий: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 0 — единица переходит в следующий разряд.
- Пятый: 0 + 0 + 1 = 1.
Вроде бы пока несложно. Так что попробуйте сами сложить 1101 и 1011, чтобы закрепить знания.
Умножаем
Что такое умножение? При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.

Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.
Умножение на 10, 100, 1000 Для того чтобы умножить целое число на 10, 100, 1000 и т. д., нужно просто дописать справа от этого числа один нуль (0), два нуля (00), три нуля (000) и т. д.

Приемы умножения. Некоторые числа легко умножать, зная особые приемы. В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.

Ход урока
I. Орг. момент:
Проверка домашнего задания.
II. Устный счет.
Учитель: вспоминаем табличное умножение и деление. Сейчас мы поиграем в игру “Почтальоны”. Света, ты будешь почтальоном. На доске домики с номерами. Твоя задача – взять пример-письмо, правильно его решить и определить в какой дом нам нужно отнести письмо.
3х4 2х2 9х2 3х1 3х8 25:5
6х2 16: 4 3х6 9: 3 6х4 5:1
4: 1 3:1
Учитель: вставьте пропущенный знак действия.
4…0=4 1…3=4 5…1=6
4…4=0 1…3=3 5…1=5
3…3=0 1…0=1 9…0=0
III. Знакомство с новым материалом
ПРО НОЛЬ
Напрасно думают, что ноль
Играет маленькую роль,
Когда-то многие считали
Что ноль не значит ничего
И, как ни странно полагали
Что он совсем не есть число.
Но о его особых свойствах
Мы поведем теперь рассказ
Коль ноль к числу ты прибавляешь
Иль отнимаешь от него
В ответе тотчас получаешь
Опять то самое число
Попав как множитель средь чисел
Он мигом сводит все на нет
И потому в произведенье
Один за всех несет ответ
А относительно деленья
Нам твердо помнить нужно то,
Что уж давно в научно мире
Делить на ноль запрещено
И впрямь: какое из известных
Число за частное нам взять
Когда с нулем в произведенье
Все числа ноль лишь могут дать
Учитель: Давай проверим, все ли в стихотворении правильно:
7+0=7 7-0=7 7•0= 0 7:0
Учитель: применим переместительное свойство умножения и заменим умножение сложением : 7•0=0•7=0+0+0+0+0+0+0=0
Что получилось?
Учитель: мы знаем, что деление проверяется умножением : тогда частное умножим на 0 – должно получиться 7, но это не возможно! Какое бы число мы не умножали на 0, всегда в произведении будет 0.
IV. Физминутка
V. Закрепление изученного материала
1. Решение задачи (с. 143 № 7)
Учитель: о чем говорится в задаче?
Ученик: о ремонте, фундаменте, кирпичах.
Учитель: что нужно узнать?
Ученик: сколько кирпичей осталось уложить.
Учитель: сможем ли мы сразу ответить на этот вопрос?
Ученик: нет.
Учитель: почему?
Ученик: потому что мы не знаем, сколько кирпичей рабочий использовал.
Учитель: сможем ли мы это узнать?
Ученик: да.
Учитель: каким действием?
Ученик: делением.
Учитель: сможем ли мы теперь ответить на вопрос задачи?
Ученик: да.
Учитель: каким действием?
Ученик: вычитанием.
Учитель: сколько же кирпичей осталось уложить рабочему?
Ученик: ( 40:5=8, 40-8=32) 32 кирпича.
2. Самостоятельная работа (с. 144 № 18)
7* 0 7:1 3* 0 8:1
7*1 0*7 0* 3 0:8
1*6 0*1 3*1 0*8
0* 6 0:1 1*3 0*1
3. Работа у доски (с. 144 № 11)
7*0 0* 8 0:5 1*3 5+0
7+ 1 0:8 6*0 1+3 5*0
7-1 8+0 8-0 4-1 5-1
VI. Повторение
1. Круговые примеры
Учитель: Мы будем лесниками. Нам надо определить высоту некоторых деревьев, для этого необходимо решить круговые примеры.
2. Арифметический диктант
Учитель: А сейчас будем стенографистами. Я диктую, а ты записываешь – стенографируешь с помощью карточек.
• Сумму чисел 45 и18 (45+18=63)
• Произведение чисел 8 и 3 (8*3=24)
• Разность чисел 35 и 7 (35-7=22)
• Частное чисел 20 и 4 ( 20:4=5)
3. Геометрический материал.
Учитель: последнее задание. Какие геометрические фигуры вы видите?
Посчитайте и скажите, сколько раз встречается каждая фигура.
(Круг – 12, квадрат – 6, треугольник – 6, прямоугольник – 5.)
VII. Рефлексия
Самостоятельное выполнение с. 144 № 17 (1,2 ст.). Ответы записаны на доске:0,0,0;5,5,5.
Оцени свою работу на уроке смайликом.
VIII. Домашнее задание
С. 144 № 12.
Порядок выполнения действий в сложных выражениях
Что важнее – умножение или сложение?
При решении примеров Расставь порядок действий. Умножить или разделить – на первом месте.
Для выражений, в которых присутствуют не сложение либо вычитание, а умножение или деление, действует то же правило: все действия с числами выполняются по порядку, начиная с левого:
Сложнее случай – когда в одной задаче встречаются умножение или деление со сложением или вычитанием. Каков порядок вычислений тогда?
Если выполнять все действия по порядку, сначала деление, затем сложение. В итоге получим:
Значит, пример решен правильно. А если в нем будут скобки?
То, что заключено в скобки, всегда в приоритете. Для того они и стоят в выражении. Поэтому порядок вычислений в подобных выражениях будет следующим:
81 : 9 + (6 – 2) + 3 = 16.
А что будет приоритетным: умножение — или деление, вычитание — или сложение, если оба действия встречаются в задаче? Ничего, они равны, в таком случае действует первое правило – действия производятся одно за другим, начиная слева.
Алгоритм решения выражения:
Ответ: 28 : (11 – 4) + 18 – (25 – ![]() = 5.
= 5.
Важно! Если в выражении есть буквенные обозначения, порядок действий остается прежним





























